Abstract
This thesis is to describe various methods for calculating the day of the week. These methods include not only the traditional methods, but also newly developed methods which enable to calculate the day instantly, called “Kurukuru Method.”
Background
What day is 2017 May 14? Not many people can answer this question. By using a calendar or searching in Google, you may find its answer, which is Sunday. However, it is very convenient to calculate the day of the week without using these tools. This thesis shows how to conduct the quick calculation of the day.
Zeller’s congruence
Zeller’s congruence is an algorithm devised by Christian Zeller to calculate the day of the week. For the Gregorian calendar, Zeller’s congruence is:
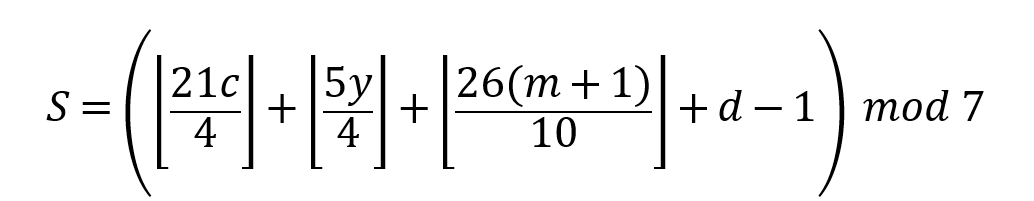
Eq. 1 Zeller’s congruence
where,
- S is the day of the week

Table. 1 S and Day correspondence
- c is the first two digits of year
- y is the last two digits of year
- m is the month, but January is 13 and February is 14.
- d is day
Zeller’s congruence cannot be solved by rote by ordinary people. The subsequent chapters describe how to get the same results as Zeller’s congruence easily.
Introduction of calculation method
Summary of methods
The following chart shows various calculation methods, which is prepared by the Author of this paper subjectively.
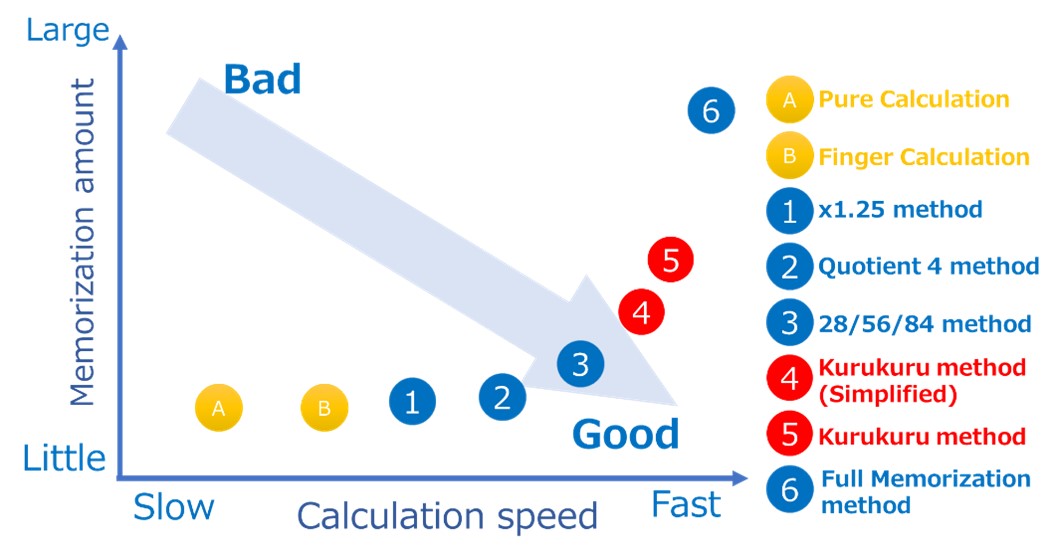
Figure 1. Various Calculation methods
X-axis represents the calculation speed, and Y-axis shows Memorization amount. The methods in right hand side enable to calculate the day quickly, which is good. The methods in the top side require a large amount of memorization, which discourage people to master the calculation methods. Therefore, the methods in Right-Down side are better than the ones in Left-Top side.
Since this type of summarization has not been conducted before, nobody has named day calculation methods. Thus, the names in the chart, such as “1.25 method”, and “Quotient 4 method” have been determined by the Author of this paper.
The methods of A, B, 1-3, and 6 whose names have not been determined can be found on the Internet. Apart from these methods, Kurukuru method is also presented in the chart. By using Kurukuru method which also has its simplified version, the fast calculation of the day can be achieved. Kurukuru method has been developed by the Author of this paper.
Pure Calculation method and Finger Calculation method
Pure Calculation method (A) and Finger Calculation method (B) are conceptually different from other methods and require lots of time to determine what day of the week. In other words, these methods are not suitable for the fast calculation of the day. These methods are briefly explained in this section below.
Pure Calculation Method
As the name implies, people calculate Zeller’s congruence (Eq.1) by using a calculator, a pen, and a sheet of paper. Since we only need to memorize the Zeller’s congruence, the memorization amount is not large. However, it takes more than one minutes to reach the answer and it is not practical to use this method for the fast calculation of the day.

Figure 2. Pure Calculation Method
Finger Calculation Method
Some of Asian people, such as Japanese and Chinese, use this technique. This method requires the sequential movement among finger nodes and joints, which results in a very long time to reach the answer. Furthermore, a mistake is easily induced in this method.
Figure 3. Finger Calculation Method
Terms and Rules
Before explaining calculation method (1) to (6), the technical terms and common rules are described.
Technical terms
In every calculation method during calculation, we need to identify (a) First 2 Digit Value (F2DV), (b) Last 2 Digit Value (L2DV), (c) Month Value (MonthV), (d) Day Value (DayV). In the case of 2020 July 14, F2DV is 0, L2DV is 4, MonthV is 5, DayV is 14. The determination method to derive each value will be described later.
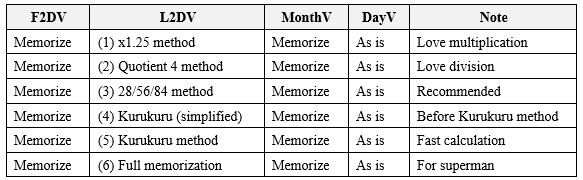
Table 2 Characteristics of each calculation method
Table 2 summarizes the characteristics of each calculation method. It is common to determine F2DV, MonthV and DayV. On the other hand, the determination method of L2DV is different among each method. In other words, the essence of day calculation is how to determine L2DV. We should select a calculation method based on our preference. For a person who is good at multiplication arithmetic, the person should use (1) x1.25 method, for a person who is good at division arithmetic, the person should use (2) Quotient 4 method. Ordinary people should use 28/56/84 method. For fast calculation, Kurukuru method is strongly recommended. If you are extremely good at memorization, (6) Full memorization method is recommended.
Common Rule
Before explaining 6 method, three rules common to every method is described below.
Rule 1: Year-Month relationship
In the case of January and February, it is regarded as “previous year”. Here are the examples:
- 1985 May ⇒ 1985
- 2031 Dec ⇒ 2031
- 2019 Feb ⇒ 2018
- 2045 Mar ⇒ 2045
- 1758 Jan ⇒ 1757
- 1900 Feb ⇒ 1899
In the third example and the fifth example, this rule is applied.
Rule 2: F2DV (First 2 Digit Value)
The year value consists of 4 digits, comprising first two digit and last two digit. For example, 1985, first two digit is “19”. F2DV is determined based on first two digit according to the table below.
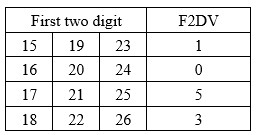
Table 3 F2DV table
Here are examples.
- May 1985 ⇒1985 ⇒ 1
- Dec 2031 ⇒2031 ⇒ 0
- Feb 2319 ⇒2318 ⇒ 1
- Mar 2545 ⇒2545 ⇒ 5
- Jan 1758 ⇒1757 ⇒ 5
- Feb 1900 ⇒1899 ⇒ 3
The table has a feature which make people memorize easily. That is, if First two digit is multiple of 4 (e.g. 16, 20, 24), F2DV is 0. If First two digit is even number and is not multiple of 4 (e.g. 18, 22, 26), F2DV is 3. If First two digit is multiple of 4 minus 1 (e.g. 15, 19, 23), F2DV is 1. If First two digit is multiple of 4 plus 1 (e.g. 17, 21, 25), F2DV is 5.
It is assumed that ordinary people naturally memorize Table 3, after several attempt of calculation.
Rule 3: MonthV (Month Value)
MonthV is determined based on the Table below.
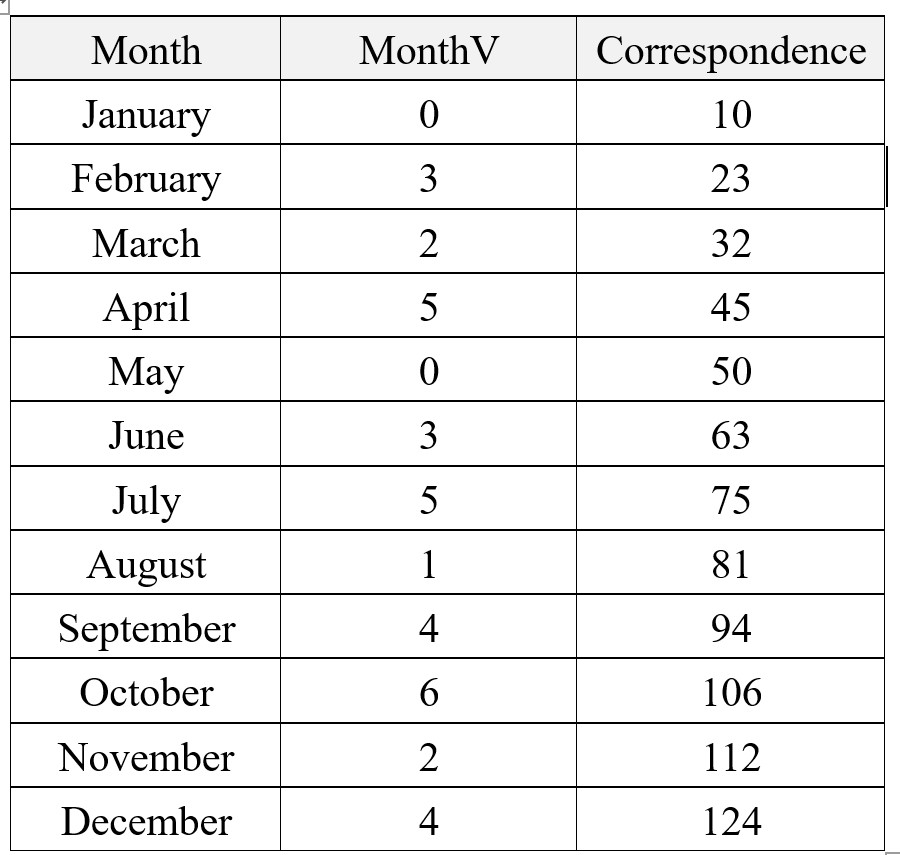
Table 4 MonthV
There are several ways to memorize the correspondences in the table above. One of them is use date. For example, if your or your family member’s birthday is February 3, you memorize “23” correspondence based on that birthday. In the same way, you should give meaning to March 2nd, April 5th, June 3rd, and so on. Another memorization method is “major system”, which will be introduced later.
Summary of rules
The following is a summary of rules described in this section.
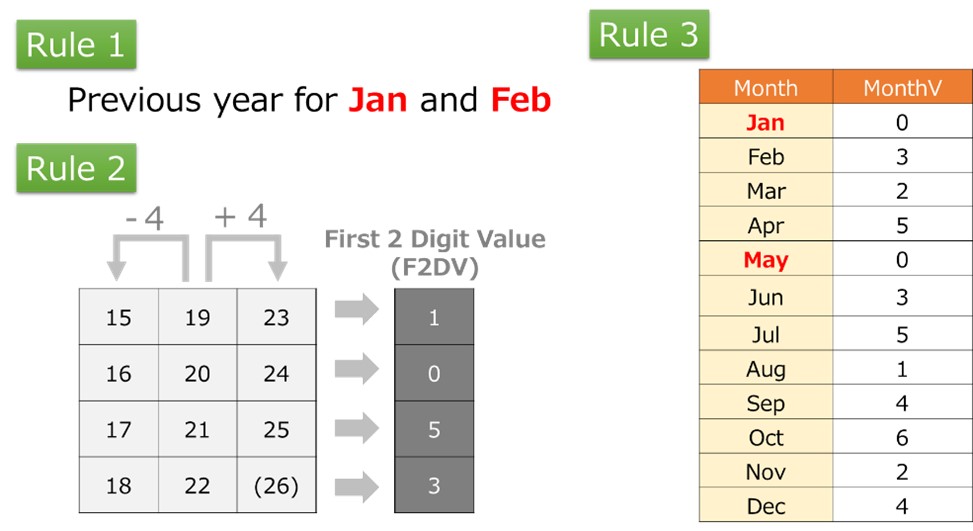
Figure 4. Summary of Rules
Calculation Methods
x1.25 method
This method is called “one point two five method”. Table 5 describes the examples of x1.25 method.
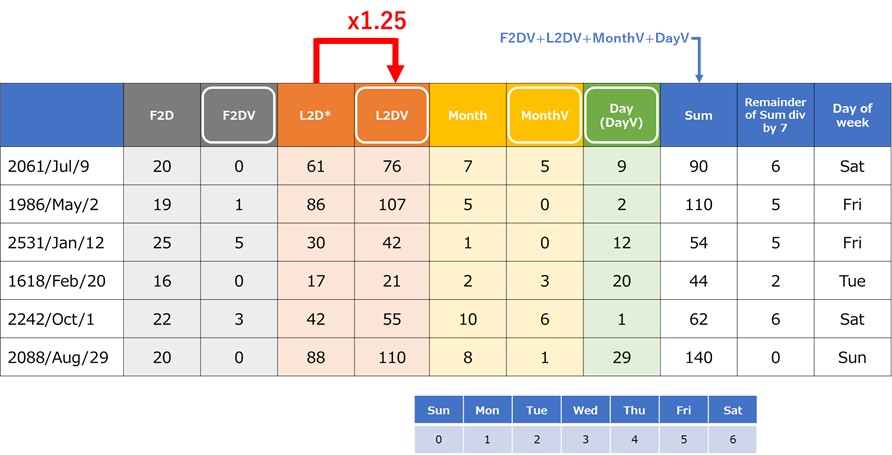
Table 5 x1.25 method
Rule 2 is applied to get F2DV, Rule 3 is applied to get MonthV, and Day value is as is. The point of x1.25 method is multiplication of Last two digit by 1.25. In the first example, 61 multiplied by 1.25 equals to 76.25. We always round down the decimals, so L2DV is 76. In the second example, 86 multiplied by 1.25 equals to 107.5 which is 107 in the table.
After determination of F2DV, L2DV, MonthV, and DayV, we add up these values. In the first example, their sum is 90, which is divided by 7, whose remainder is 6. This remainder corresponds to the day of the week, which is Saturday.
In the same way, other examples can be calculated. It is noted that in the third example and the fourth example, we have to reduce the value of year by one because they are January and February. In the third example, Last two digit is not 31, but 30. In the fourth example, Last two digit is not 18, but 17.
Since this method require multiplication of 1.25, most of us requires to use a calculator. Therefore, unless you love multiplication, this method is not recommended.
Quotient 4 method
Quotient 4 method is relatively easier than x1.25 method. Table 6 describes the examples of quotient 4 method.
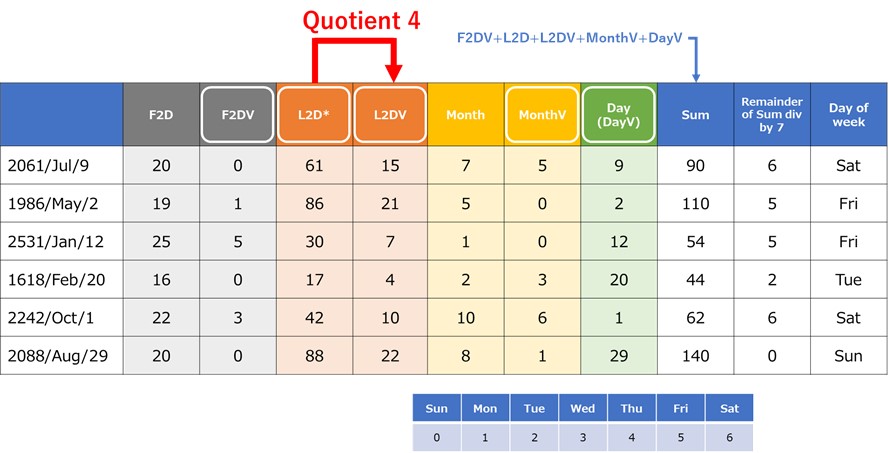
Table 6. Quotient 4 method
Same as x1.25 method above, Rule 2 is applied to get F2DV, Rule 3 is applied to get MonthV, and Day value is as is. The point of Quotient 4 method is division of Last two digit by 4. In the first example, 61 divided by 4 equals to 15.25, which will be rounded down to 15.
After determination of F2DV, L2DV, MonthV, and DayV, we add up Last two digit and these values. We will get the same total value as one of x1.25 method, 90. The total value is divided by 7 and its remainder, 6, represents the day of the week, Saturday. The rest of the examples can be calculated in the same way.
Ordinary people think that this method is easier than x1.25 method, since the multiplication of 1.25 is more difficult than division of 4. However, this method is still troublesome.
28/56/84 method
For the day calculation learner, this method is highly recommended.
When Last two digit is small number, Quotient method works very well because the calculation burden is not very high. However, if Last two digit is big number, ordinary person will have difficulty in mental calculation. 28/56/84 method eases this problem.
The principle behind is to convert Last two digit to an equivalent and small number by using one of 28, 56, and 84.
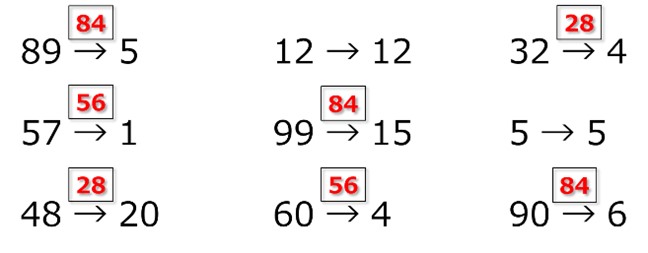
Figure 5. Preprocessing of 28/56/84 method
As seen in Figure 5, the Last two digits are reduced to small numbers. For instance, 89 is converted to 5. In calendar calculation, 89 and 5 are mathematically equivalent.
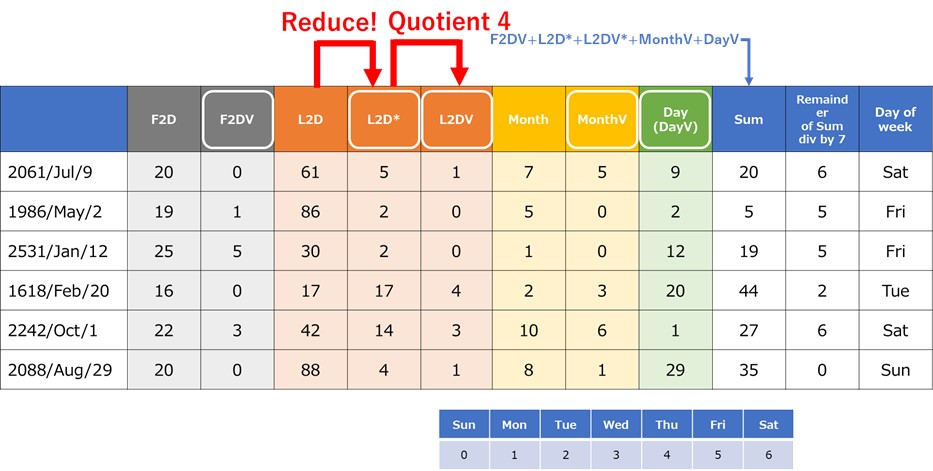
Table 7 28/56/84 method
28/56/84 method is basically same as Quotient 4 method apart from the preprocessing of Last two digit. In the first example, Last two digit 61 is preprocessed by using 56 to 5. This preprocessed value 5 is divided by 4 and its quotient is 1. We are adding up 0 (F2DV), 5 (Last two digit), 1 (L2DV), 5 (MonthV), and 9 (DayV). The total is 20. This is divided by 7 and its remainder 6 corresponds to Saturday. In Quotient 4 method, we have to add up 0, 61, 15, 5, and 9, which are too big to calculate easily. Even though 28/56/84 method requires extra subtraction compared to Quotient 4 method, it will realize easy calculation and avoid miscalculation.
Full memorization method
As described before, the essence of the day calculation is “how to calculate L2DV”. If we memorize all of L2DV and recall them, we do not need to process any calculation in our brain. This is Full memorization method.
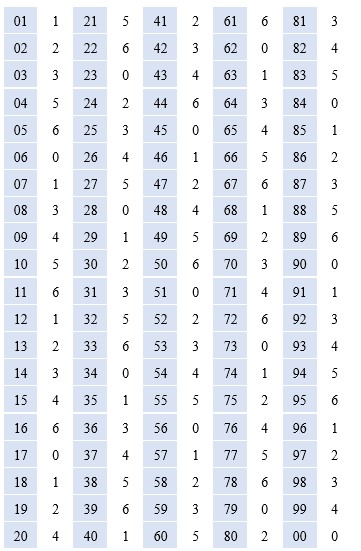
Table 8. L2DV table
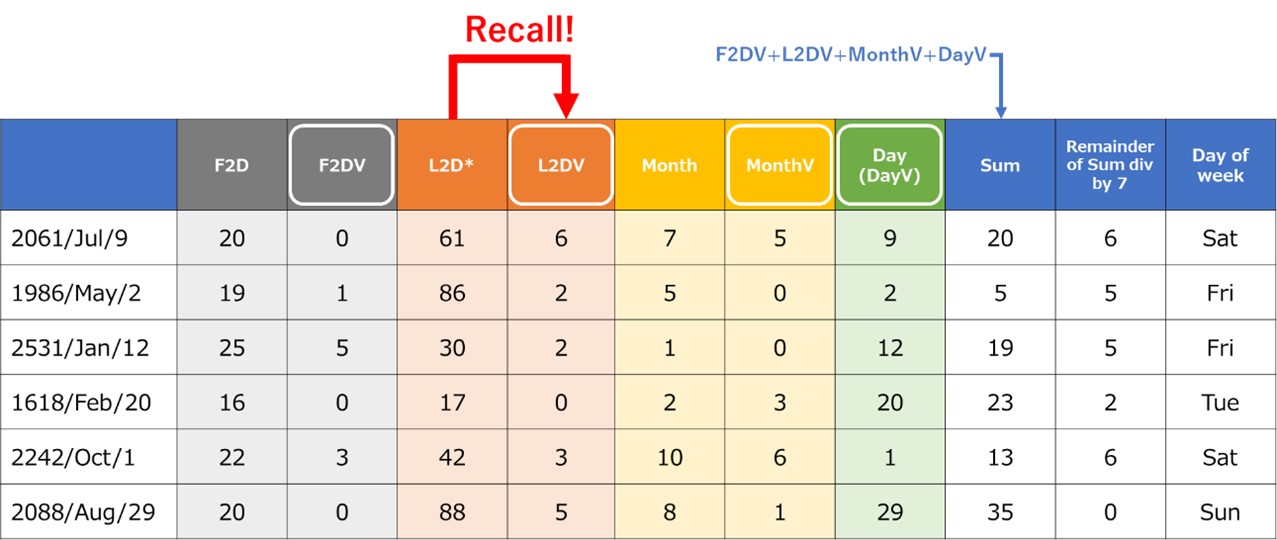
Table 9. Full memorization method
Table 9 describes the examples of Full memorization method. In order to obtain L2DV, we merely recall L2DV. It would take a great deal of training to achieve this memorization. Ordinary persons may think this method is for someone who has special talent.
Kurukuru method
Kurukuru method introduction
Kurukuru method has been being developed by Author of this paper. Its methodology is still being studied and applied to other fields. “Kurukuru” is named after Speed Cubing Club which is organized by Author of this paper.
Figure 6. Kurukuru is based on Memory Sport
Kurukuru method utilizes some techniques of memory sport. Memory sport refers to competitions in which participants attempt to memorize then recall different forms of information, under certain guidelines. Memory sport has various competition event, such as playing card, number, names, and so on.
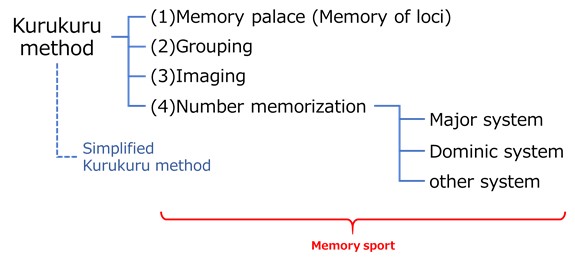
Figure 7. Kurukuru method and Memory sport
Memory palace
Memory palace (aka. Memory of loci) is frequently used in Memory sport. This is very useful technique for memorization. The human brain has an excellent ability to memorize visualized things by associating them with location information.
At first, we decide own 7 places. Each place has a unique number from 0 to 6.
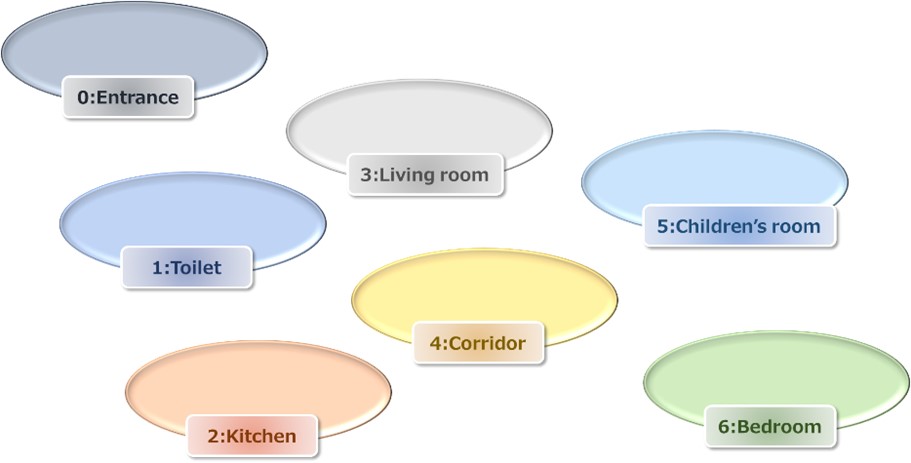
Figure 8 Example of 7 places
Figure 9 Another example of 7 places
It is recommended to select seven familiar places. They should be distinguishable. For instance, the selection of both “high school” and “elementary school” is not advised since their images are overlapped (e.g. places to study).
Number association
In each place, the fixed numbers are associated. These fixed numbers are Last two digits. For instance, Place 0 is associated with 00, 06, 17, 23, 28, 34, 45, 51, 56, 62, 73, 79, 84, and 90. Other places have their own unique numbers. This association is equivalent to the correspondence in Table 8, which is used in Full memorization method.
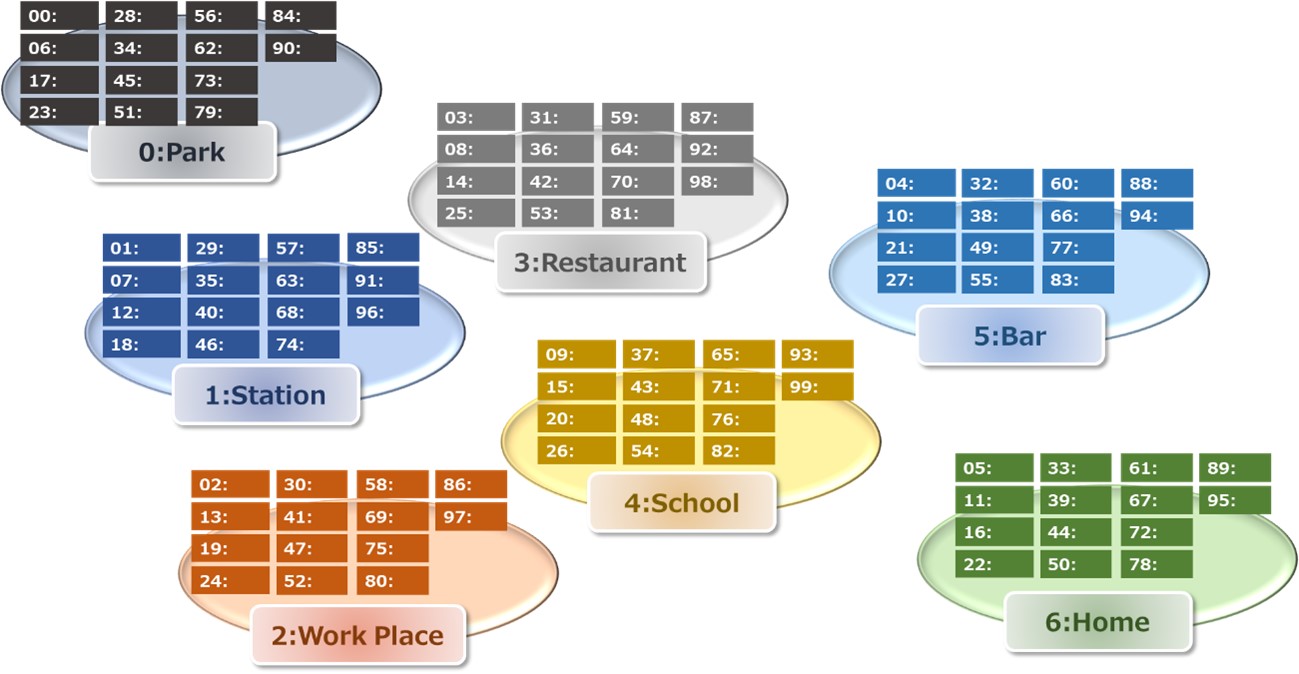
Figure 10. 7 places associated with Last two digits
Number memorization
It will be very difficult to memorize the association of Figure 10. This is because a number itself has no meaning. A technique of Memory Sport will give us its solution. There are several ways to memorize numbers, for instance, Major system, Dominic system, Play on words, and so on. For Japanese and Chinese, Play on words is the best technique to memorize numbers. For English speakers, Major system is a common technique to memorize numbers.
The major system is a mnemonic technique used to aid in memorizing numbers. The system works by converting numbers into consonants, then into words by adding vowels. The system works on the principle that images can be remembered more easily than numbers. There are lots of websites introducing Major system, so it is recommended to refer to them. Major system help you memorize any numbers, such as credit card number, telephone number, birthdays of all of your friends, and so on. If you have not mastered it, I strongly recommend you start master this technique to enrich your life!
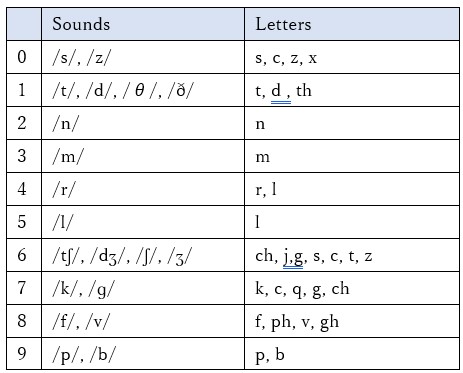
Table 10. Major System table
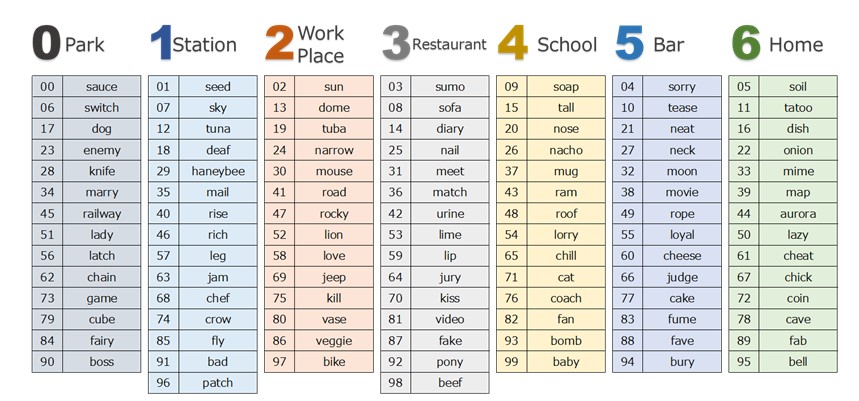
Table 11. Example of major system applied to Kurukuru Method
Table 11. shows an example of Major system table applied to Kurukuru Method. Based on this table, we memorize the “visualized” object/action in each place. For instance, there are source (00), switch (06), dog (17), enemy (23) in Park (0). This means that if Last two digits are 00, 06, 17, or 23, L2DV is 0. In the same way, we can associate Last two digits to L2DV in other places.
We can prepare our own Major system table according to individual preference. There are several tips in doing this. One of them is to avoid overlapped images. For example, lion (52) and puma (93) are conceptually similar, so they may be mistaken. Furthermore, we should use “unfavorite” object/person’s name for Major system table. This is because our brain may keep the unfavorite things rather than favorite things.
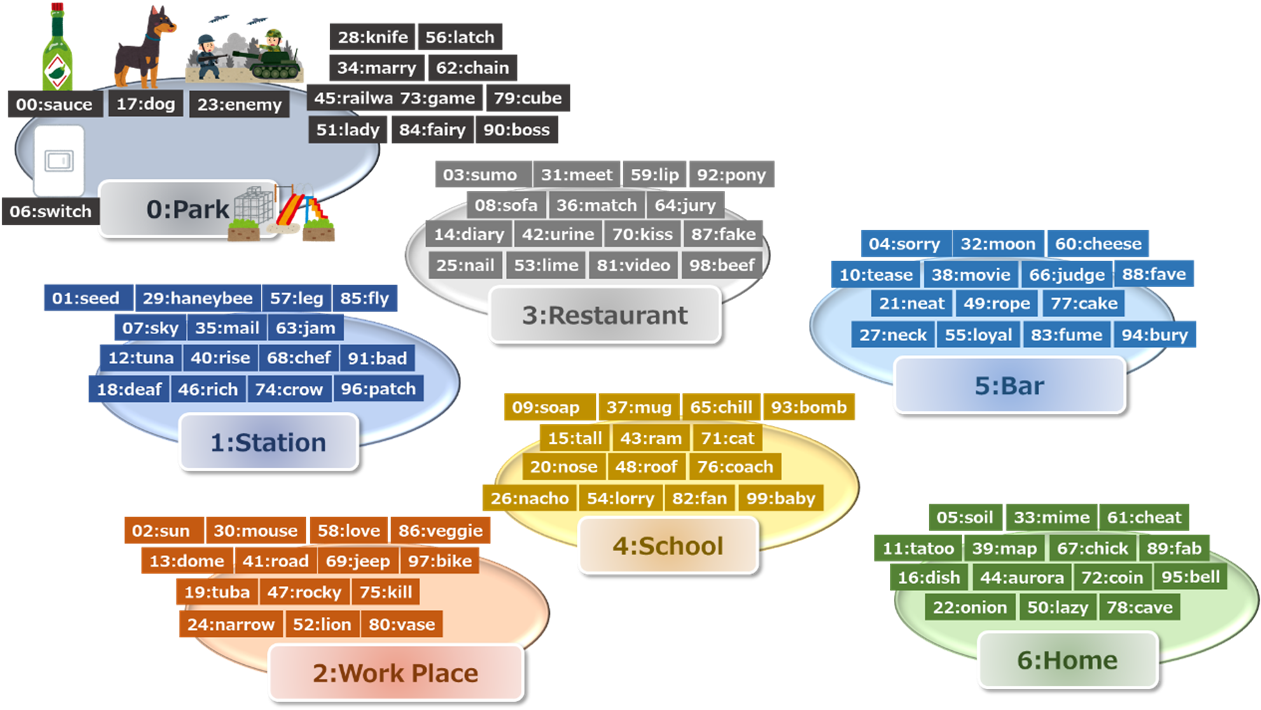
Figure. 11 Visualized Major System (only partially visualized)
It is noted that this Kurukuru Method exploits the properties of the brain, where are:
- easy to memorize in association with places
- easy to memorize in groups
- easy to memorize visualized objects
Application of Kurukuru Method
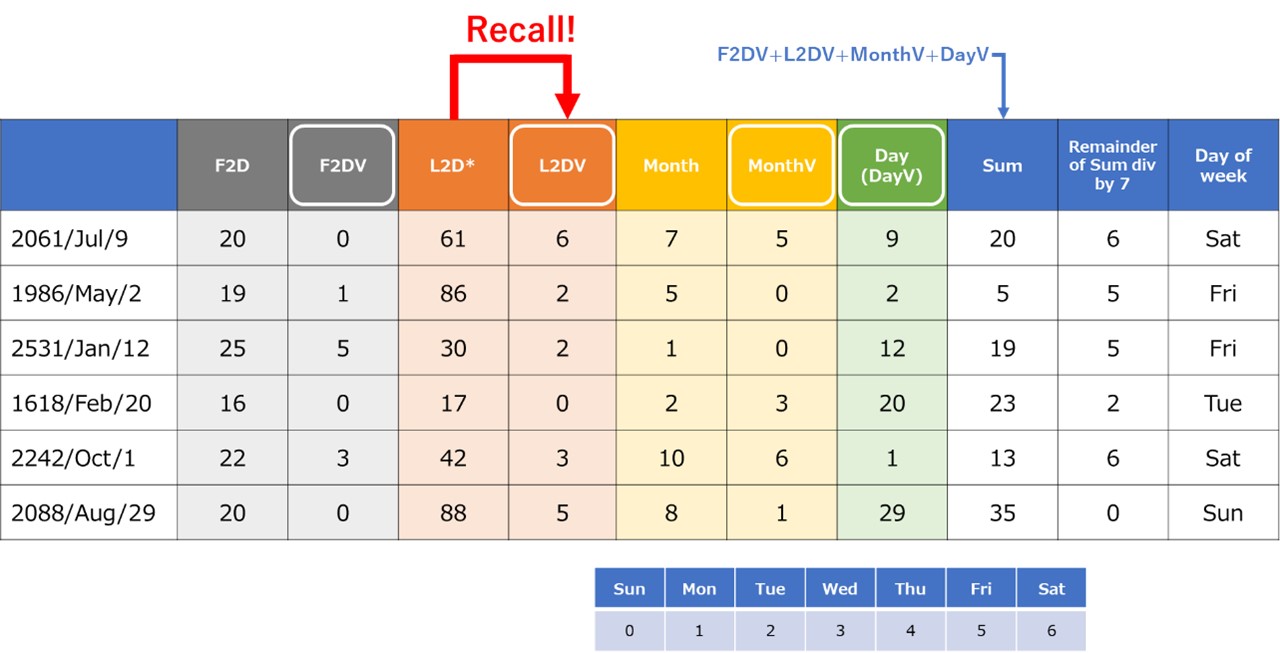
Table 12. Kurukuru method
Table 12 describes the examples of Kurukuru method. Same as Full Memorization method, L2DV is recalled directly from Last two digits. In the first example, Last two digit is 61, which is “cheat” in “Home (6)”. Therefore, 6 for L2DV is directly retrieved. In the same way in the second example, Last two digit is 86, which is “veggie” in “workplace (2)”
Kurukuru method requires the memorization of 100 objects. Therefore, it will take long time to master it. Therefore, it is recommended to start from Simplified Kurukuru method described in the next chapter.
Simplified Kurukuru method
One of the drawbacks of Kurukuru method is to memorize 100 objects. It is too many for the beginners. In order to reduce the number of objects for these people, a preprocessing is conducted using 28/56/84 method.
Figure. 12 Simplified Kurukuru method
When Last two digit is more than 28, a subtraction is conducted by using one of 28, 56, and 84. (See Figure. 5) As a result, the number of objects is reduced from 100 to 28. (See Figure. 13)
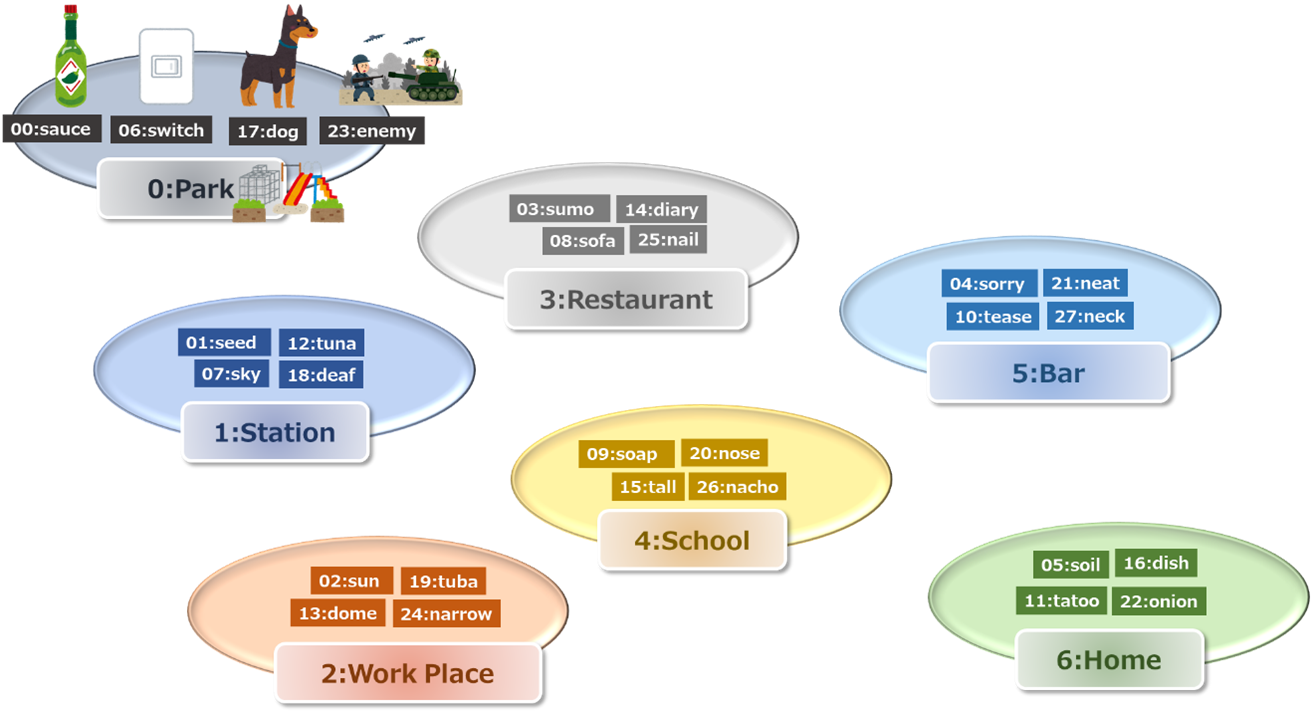
Figure. 13 Visualized Major System (only partially visualized)
Table 13 describes the examples of Simplified Kurukuru method. Same as 28/56/84 method, a preprocessing, which is the subtraction of 28/56/84, is conducted before recalling. By doing this, we do not need to memorize 100 objects in advance.
At the beginning stage of mastering Kurukuru method, it is recommended to start from Simplified Kurukuru method.
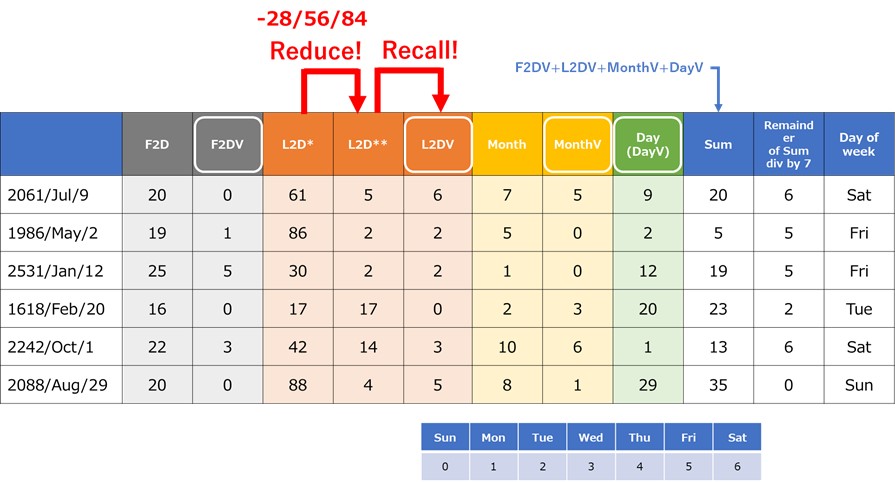
Table 13. Simplified Kurukuru method
Calculation technique
There are several techniques to realize the fast calculation. The order of calculation should be DayV, MonthV, L2DV, and F2DV. This is because it is easy to adjust Last 2 digit in case of January and February. During this process, we find the lucky parts in Date, which corresponds to Zero calculation. See Fig. 14.
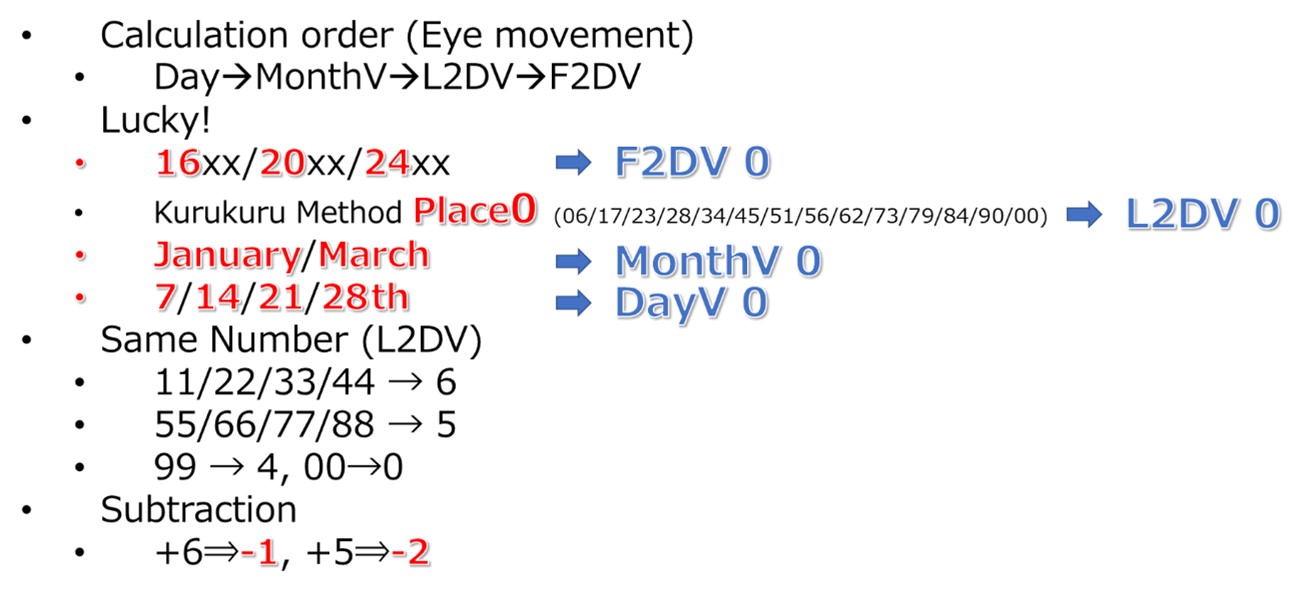
Fig. 14 Calculation tips
For instance, 14 May 2017, F2DV is 0, L2DV is 0, MonthV is 0, and DayV is 0. Therefore, the day of this date is Sunday.
Another technique is related to Same number (doublets). Visually, same numbers can be identified easily. L2DV for small same numbers (11, 22, 33, and 44) is 6, one for large same numbers (55, 66, 77, and 88) is 5. L2DV for 99 is 4 and one for 00 is 0.
Further technique is heptadecimal notation. For some people, including Author of this paper, can subtract 1 much faster than add 6. Some people think that Subtraction of 2 is better than addition of 5.
You will be able to conduct faster calculation using these techniques.
Speed-Calendar.com
Speed-calendar.com is run by the son of Author of this paper, supported by Author. Speed-calendar.com provides various services:
- Publication of calculation technique:
- Offer of education opportunities:
- Organizing of tournament:
- Promotion of community
- Provision of program software


5.1 Program software
Speed-calendar timer
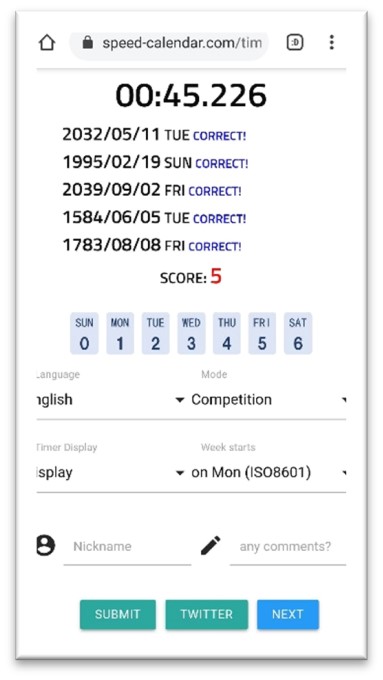
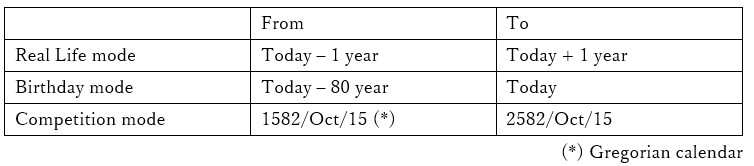
Table. 14 SpeedCalendar timer
Other software
There are several software which is related to day calculation.


Note about Zeller’s congruence (h, D)
In this thesis, the remainder 0 corresponds to Sunday. It is noted that other systems are used in computer science as described Table 15.

Table 15. Notation of Day
Summary
This thesis describes various methods for calculating the day of the week. A newly proposed method, “Kurukuru method” is also proposed therein. I hope you enjoy the content of this thesis and you join our activities, such as SpeedCalendar competition.
Thanks.
Yuichi Hamada, a support of SpeedCalendar
A thesis corresponding to this page is uploaded to Github.
